[Update, April 13, 2007: Thanks to Herr Ziffer for catching a confusing typographical error.]
I can’t believe I’d never seen (or figured out) this quick method for converting a binary number to a decimal number in your head. All you need to be able to do is double numbers and occasionally add one.
- Start at the first ‘1’ on the left, and start with the mental number one
- Move one digit right. If that digit is a zero, multiply your mental number by two. If it is a one, multiply your mental number by two and add one.
- Repeat step 2 for every digit of the binary number
Here’s an example. We’ll use the binary number 1101010 1011010:
- 1011010 – We start at the first one. Our mental total: 1
- 1011010 – Next digit is a zero; we double our mental number: 1 x 2 = 2.
- 1011010 – Next digit is a one; we double our mental number and add one: 2 x 2 + 1 = 5
- 1011010 – Another one; double and add one: 5 x 2 + 1 = 11
- 1011010 – Zero; double: 11 x 2 = 22
- 1011010 – One; double and add one: 22 x 2 + 1 = 45
- 1011010 – And finally a zero; double: 45 x 2 = 90
The rest of this post is a little more technical, so if you glazed over when reading the above, it now may be time to soothe your tired mind.
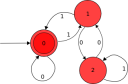 I happened across this trick while contemplating a three-state discrete finite automaton that identifies binary numbers divisible by three. The automaton starts in state 0, and like the above procedure starts at the left side of the number. The number of the state can be thought of as the remainder of the number as read so far, mod 3. Every time a zero or a one is read, the automaton follows the arrow with that label from its current state. If it ends in state 0, the number is evenly divisible by three. Once I understood why the DFA actually works, the mental calculation became glaringly obvious.
I happened across this trick while contemplating a three-state discrete finite automaton that identifies binary numbers divisible by three. The automaton starts in state 0, and like the above procedure starts at the left side of the number. The number of the state can be thought of as the remainder of the number as read so far, mod 3. Every time a zero or a one is read, the automaton follows the arrow with that label from its current state. If it ends in state 0, the number is evenly divisible by three. Once I understood why the DFA actually works, the mental calculation became glaringly obvious.
For even more fun, the regular expression (0*(1(01*0)*1)*)* will also match binary numbers divisible by three.
Exciting! Now you have something to talk about the next time you go to a cocktail party.

