Categories
computer science mathematics mental exercises

Quickly Convert Binary to Decimal in Your Head

[Update, April 13, 2007: Thanks to Herr Ziffer for catching a confusing typographical error.]

I can’t believe I’d never seen (or figured out) this quick method for converting a binary number to a decimal number in your head. All you need to be able to do is double numbers and occasionally add one.

  1. Start at the first ‘1’ on the left, and start with the mental number one
  2. Move one digit right. If that digit is a zero, multiply your mental number by two. If it is a one, multiply your mental number by two and add one.
  3. Repeat step 2 for every digit of the binary number

Here’s an example. We’ll use the binary number 1101010 1011010:

  • 1011010 – We start at the first one. Our mental total: 1
  • 1011010 – Next digit is a zero; we double our mental number: 1 x 2 = 2.
  • 1011010 – Next digit is a one; we double our mental number and add one: 2 x 2 + 1 = 5
  • 1011010 – Another one; double and add one: 5 x 2 + 1 = 11
  • 1011010 – Zero; double: 11 x 2 = 22
  • 1011010 – One; double and add one: 22 x 2 + 1 = 45
  • 1011010 – And finally a zero; double: 45 x 2 = 90

The rest of this post is a little more technical, so if you glazed over when reading the above, it now may be time to soothe your tired mind.

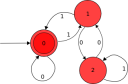Discrete finitite automaton to identify binary numbers divisible by threeI happened across this trick while contemplating a three-state discrete finite automaton that identifies binary numbers divisible by three. The automaton starts in state 0, and like the above procedure starts at the left side of the number. The number of the state can be thought of as the remainder of the number as read so far, mod 3. Every time a zero or a one is read, the automaton follows the arrow with that label from its current state. If it ends in state 0, the number is evenly divisible by three. Once I understood why the DFA actually works, the mental calculation became glaringly obvious.

For even more fun, the regular expression (0*(1(01*0)*1)*)* will also match binary numbers divisible by three.

Exciting! Now you have something to talk about the next time you go to a cocktail party.

51 replies on “Quickly Convert Binary to Decimal in Your Head”

Paul,

You had me scratching my head for ten minutes wondering why I couldn’t do the conversion. It appears you have a typo: “We’ll use the binary number 1101010” should be “We’ll use the binary number 1011010”.

With this, I intend to startle my friends and seduce my enemies at the next cocktail party.

Thanks. 🙂

Aargh! I thought I’d triple-checked everything!

This is a good warning, though: misapplied, you can also use this trick to embarrass yourself publicly. Thanks, Herr Z.

By Post Author

thank you so much!! Will be very much helpful in my exam which is in 1 day time lol…

hey buddy u are simply great. please tell me the trick that how did u calculate the regu;ar expression is there any trick????

Hi, Sumitra. Regular expressions and discrete finite automata are equivalent; that is, they both are able to recognize the same class of “languages”. A theory of computation textbook should explain this equivalence in detail (Michael Sipser’s Introduction to the Theory of Computation, for example). There are a lot of lecture slides online that explain the process of converting one to another….http://www.math-cs.gordon.edu/courses/cps220/Notes/regular_expressions.pdf gives a decent overview.

By Post Author

Do you have any tips on converting Decimal to Hex or binary in head?

(please notify me via email, if you happen to have a solution)

Hi, AIbY,

This trick can be used in reverse for converting decimal to binary, but it’s harder to do mentally as the binary numbers tend to overflow your mental registers. If you try it, it’s best to use a piece of paper and write the binary number down as you go. You’ll be writing down the digits from right (least significant) to left (most significant).

So, the procedure looks something like:

1. Start with the decimal number in your head
2. Is the current decimal number divisible by 2?
a. If so, then write down 0
b. If not, then write down 1 and subtract 1 from the mental number.
3. Divide your mental number by 2 and go back to step 2. Repeat until your mental number is 0.

It’s easy to lose track of where you are in the conversion process, so jotting notes is helpful.

Directly applying this process to hexadecimal is even harder, as it relies on the ease of dividing by two. One possible approach would be to first convert your decimal number to binary as described above and then converting each set of four binary digits to hex, starting from the right…easy enough, just memorize your single-hex-digit-to-binary conversion table.

By Post Author

Hello,

First off I’d like to say, this is gold! I am studying for my CCNA and CCNP and your method will go a long way in helping me to succeed.

I have one question though.

I’ve tried to follow your steps with the decimal 55 and have had no luck with your convertion method. The binary I should end up with is “00110111”, but I endup with “010010101”. Can you please help me out with an example of how to do it? I think I’m doing it worng.

Thank you in advance!!

Regards,
Javier

JavierVV,

I hadn’t looked at this for a while, and I was confused myself for a minute!

The tricky thing in the way those steps are written is that step 3 (dividing the mental number by 2) is always performed. After step 2, whether you’ve performed 2a or 2b, the mental number will always be even…so you’ll always be able to divide by 2 and get an integer as a result.

Also, the digits are written from right to left…this means, for any positive integer, the last digit you write will always be a 1!

So:

(2) -> 55 is not divisible by 2
(2b) -> new binary is 1, 55-1 = 54
(3) -> 54/2 = 27
(2) -> 27 is not divisible by 2
(2b) -> new binary is 11, 27-1 = 26
(3) -> 26/2 = 13
(2) -> 13 is not divisible by 2
(2b) -> new binary is 111, 13-1 = 12
(3) -> 12/2 = 6
(2) -> 6 is divisible by 2
(2b) -> new binary is 0111
(3) -> 6/2 = 3
(2) -> 3 is not divisible by 2
(2b) -> new binary is 10111, 3-1 = 2
(3) -> 2/2 = 1
(2) -> 1 is not divisible by 2
(2b) -> new binary is 110111, 1-1 = 0
(3) -> mental number is 0 and conversion is complete

The converted binary is, therefore, 110111.

By Post Author

WOW this is really awesome i have tried the method and its reverse
thanks Herr Ziffer
thanks Pual

But, I still dont understand how DFA works. Pls, explain it to me. Thank you very much. 🙂

I know this was posted years ago, buuuuut, I’ve been struggling with learning binary to decimal in my UNI studies – the text book and lectures have confused me…and thanks to you I have NAILED it…if I could hug you I would…Jane.

Thanks for the hint! And you can do it to an auctioneer’s chant to make it stick. At least, that helps me keep track in my own head.

There’s a one, zero double it two. There’s a one, double it four, add one, now we’re at five. Five, there’s a one, double it ten and add a one, we’ve got eleven eleven. There’s an O, double it TWENNY two. Got a one, double it fourty four add one that’s fourty five, now a zero double it Ninety SOLD.

WOW you just saved my life. I was struggling to understand the conversion. Always been bad at math. But this trick makes it so easy.

Thanks

Sir,Thank you so much.Now i need to know the easiest way to converting from decimal to binary.it would be highly appreciate if you could do something for me….

Someone convert 10010101010000101010101001010101010011001010100010000001010101 to decimal with each step listed for review. Thanks in advance.

hey friends , for converting 4 digit binary number to decimal , there is a simple method which we can do by seeing,
lets learn by an example:
convert (1001)binary to decimal
first we know 8421 is the basic code for writing decimal numbers;
just compare
8421 with
1001
here we got 1’s at 4th and 1st position in 8421
so add 8 and 1 i.e.,
8+1= 9 is the decimal number.
another example
1111
8421
so we got 1’s at all the positions in 8421
so add 8,4,2,1 i.e., 8+4+2+1=15 is the decimal number.

Thanks Buddy..I was confused with these digits.You made it simple by this way.Thanks a lot..

God lord thank you for your hard work man! helped a lot…

how many such DFA’s that compute integers of mod 3 do you reckon exist?

will this method still works even when your using higher number in binary … for example I got 2^26 … kinda hard to use if thats the number

i like your short cut no need to multiply it by itself many time then add later on /.. thanks

Oh i want to add one more thing to it .it is something that computer’s usually do.as an example
Suppose : binary string is 1011 and you want to find it’s value by program

then Start_Num=1(LeftMost Bit)
for each step
if that bit is 0 you do Start_Num<<1
else you do Start_Num<<1 + 1

I know another way that is slower because it’s adding instead of multiplying. However it should be much simpler in the case of converting a decimal into binary.

The method works from the right to the left. The value of that number is 1. Ignore the value if the decimal has a “0” or add 1 if the decimal has a “1”. Moving leftward the value doubles. So the second number of the right either has a value of 2 or a value of 0 (if the decimal is 0). Add that to your total. Move leftward again one place and the value is either 4 or 0. Again and it’s 8 or 0. Keep adding until you are done.

Using the example: 1011010
0 + 2 + 0 + 8 + 16 + 0 + 64 = 90

And to convert from decimal into binary:

Find the highest value number that goes into 90 without exceeding 90. 128 goes over so 64 it is. Put a 1 on the left side of your binary number to symbolize 64. Now half the number and if it exceeds the decimal number then put a 0, if not then add a 1 to symbolize that number. In the case of 90: 64 + 32 = 96 … So the next is a 0. Move on to 64 + 16 = 80. Add a 1 to symbolize 16. Move on to the next value of 8. 80 + 8 = 88. Add a 1 to symbolize 8. Move on the value of 4. 88 + 4 = 92. Add a 0 to symbolize 0. Move on to the value of 2. 88 + 2 = 90. Add a 1 to symbolize 2. Move on to the final value of 1. 90 + 1 = 91. Add a 0 to symbolize 0.

This version is easier to convert decimal into binary however the method from this site is more useful for converting binary into decimal.

Hii. This is cool one question tho. What if the number starts with zero? do we multiply it right away to 2 and then add 1?
like 1 * 2 + 1?? or we still start at 1?

change that. i made a mistake. i mean if the binary starts at zero do I still start at 1* 2 and then proceed to the next digit?

Hi, Rei.

Just as with decimal numbers, you can assume there are an infinite number of zero to the left of the leftmost binary digit. So, If you have a binary number with extra 0s on the left, just ignore them and start with the first 1.

By Post Author

it wont work if the binary number is 00001111
Working:
1 x 2 = (2) + 1 = 3
3 x 2 = (6) + 1 = 7
7 x 2 = (14) + 1 = 15
thus 1111 is note equal to 16 in decimal. There seems to be some major loop hole.
please correct me if im wrong.

After getting hacked (five or six years ago!) I just shut down the blog rather than slogging through the code trying to get things rooted out. But, everything is still here, including a handful of unapproved comments. So, four years later: you’re right in your calculation, Bazy, but 1111 binary is, in fact, 15. 16 would be 10000.

By Post Author

That was a wonderful method..just helped me a lot.it just made my confusion get vanished…

Hi Paul,

This calculation is just fantastic, thank you so much as it has saved my life!

One thing I found is it does not appear to convert 11111111 correctly, it should convert to 255 in decimal but I keep getting 248 for some reason, could you please advise what I’m doing wrong?

Again, finally getting around to fixing up this blog and approving the few non-spam comments among the chaff. Since you didn’t show your calculation I can’t be quite sure what you’re doing wrong, but there’s a clue in that your result isn’t odd. If your current number is a 1, you will always be adding a 1 after the doubling. So:
1
(1) x 2 + 1 = 3
(3) x 2 + 1 = 7
(7) x 2 + 1 = 15
(15) x 2 + 1 = 31
(31) x 2 + 1 = 63
(63) x 2 + 1 = 127
(127) x 2 + 1 = 255

By Post Author

Again, finally getting around to fixing up this blog and approving the few non-spam comments among the chaff. Since you didn’t show your calculation I can’t be quite sure what you’re doing wrong, but there’s a clue in that your result isn’t odd. If your current number is a 1, you will always be adding a 1 after the doubling. So:
1
(1) x 2 + 1 = 3
(3) x 2 + 1 = 7
(7) x 2 + 1 = 15
(15) x 2 + 1 = 31
(31) x 2 + 1 = 63
(63) x 2 + 1 = 127
(127) x 2 + 1 = 255

By Post Author